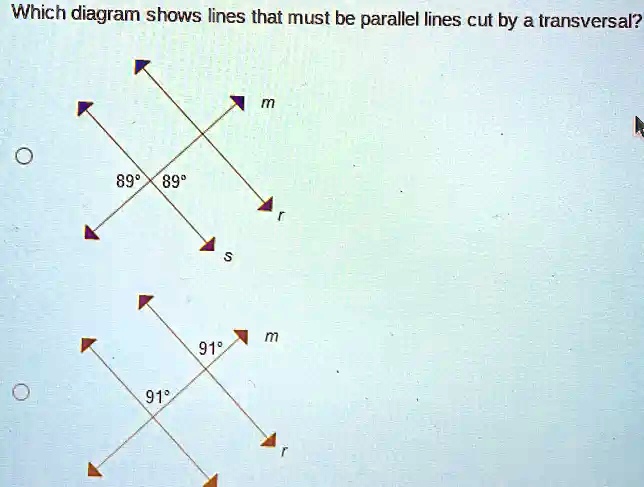
Have you ever looked at a picture with lines and a slanted one crossing them? You need to figure out which diagram shows lines that must be parallel lines cut by a transversal. This question pops up a lot in geometry homework. It helps to see if you know how angles work together.

A transversal line geometry cuts across two or more lines. When those lines are parallel lines cut by a transversal, special angle pairs match up. This helps you prove the lines stay the same distance apart. In this guide, we break it down step by step¹. You will learn to pick the right diagram every time.

Students in grades 8-10 meet this for the first time. It builds on basic geometry line and angle relationships. Do not worry if it feels new. We use easy words and examples. By the end, you will spot identifying parallel lines like a pro. For more on line basics, see our guide on five surveying tools.

Key Angle Pairs in Parallel Lines Cut by a Transversal

Start with the basics. Picture two straight lines. A third line, the transversal, crosses both. This makes eight angles at the two crossing points.

The magic happens with parallel line relationships. Certain angles become equal or add to 180 degrees. These are the properties of parallel lines. Here are the main pairs:

• Corresponding angles theorem: These sit in the same spot on each line. For example, the top-left angle on the first line matches the top-left on the second. If they equal, the lines must be parallel.
• Alternate interior angles: These are inside the lines but on opposite sides of the transversal. Equal ones prove parallel.
• Same-side interior angles: Also inside, but on the same side. They add to 180 degrees for parallel lines.
• Alternate exterior angles: Outside the lines, opposite sides. Equal for parallel.

These come from Euclidean geometry. The parallel postulate says one transversal makes these matches only if lines never meet.

Why care? It helps in proving lines are parallel. Look for angle congruence. If angles match as above, the diagram shows parallel lines cut by a transversal. Check related math concepts in Wentworth Institute of Technology programs.

How to Check a Diagram for Parallel Lines

Follow these steps to answer which diagram shows lines that must be parallel lines cut by a transversal. Grab a pencil and paper to sketch.

1. Find the transversal: Spot the line crossing the other two. It is often slanted.
2. Label the angles: Number them 1 to 8. Start at the top intersection, go clockwise.
3. Look for matching pairs: Check corresponding angles. Are they the same number? Do the same for alternate interior angles.
4. Check supplements: For same-side interior angles, add them. Do they make 180?
5. Decide: If one pair fits the rule, the lines must be parallel. No match? They might intersect.

This step-by-step method to find parallel lines cut by a transversal works for any picture. It uses geometric reasoning. Explore more reasoning in math problem-solving tips.

Real Diagram Examples to Practice

Let us look at common diagrams. These match ones on sites like Brainly or Quizlet². We explain why some work and others do not.

Example 1: Two horizontal lines. Transversal slants right. At the top intersection, bottom-left angle is 115°. At the bottom intersection, upper-left is 65°.

• These are corresponding angles. 115° ≠ 65°. Not parallel.

Example 2: Same setup. Top intersection: bottom-left 115°, bottom-right 65°. Bottom intersection: no clear match.

• Bottom-right and something else? No full pair. Angles on one line add to 180, but that is straight line, not parallel proof. Skip.

Example 3: Top intersection: top-right 115°. Bottom intersection: upper-left 115°.

• These are corresponding angles. Both 115°. Yes! This diagram shows lines that must be parallel lines cut by a transversal.

Example 4: Top: upper-left 65°, bottom-right 65°. Bottom: no info.

• Possible alternate interior angles? Need both intersections. Incomplete.

Practice with geometry diagrams. Draw your own. Change one angle. See what breaks the parallel rule. For fun practice, try Lethal Company mods for geometry-like puzzles.

Common Mistakes and How to Avoid Them

Kids mix up pairs. Here is how to stay on track:

• Do not confuse corresponding with vertical: Vertical angles are opposite at one spot. They are always equal, but do not prove parallel.
• Check both sides: One pair is enough, but confirm no tricks.
• Watch for supplementary angles: Supplementary angles add to 180. Good for same-side, not always corresponding.
• Use color: Highlight pairs in transversal intersections. Red for corresponding, blue for alternate.

This avoids errors in math problem-solving. See error fixes in code error guides.

Why Angles Prove Parallel Lines

Go deeper. The corresponding angles theorem is a big deal. It says: If a transversal cuts two lines and corresponding angles equal, then the lines are parallel.

Proof sketch (easy version):

1. Draw parallel lines (assume for now).
2. Transversal crosses.
3. Corresponding angles match because of parallel postulate.

Reverse it for your question. Equal angles force parallel.

Same for alternate interior angles. They are like corresponding but flipped.

In angles formed by parallel lines, you see:

• Equal corresponding = parallel.
• Equal alternate interior = parallel.
• Same-side interior 180° = parallel.

This is key for what angles prove two lines are parallel in geometry. Dive into proofs at geometry proofs resources – wait, better: logical reasoning.

Fun Ways to Remember the Rules

Make it stick:

• Corresponding: “Same corner buddies.”
• Alternate interior: “Zig-zag inside.”
• Same-side: “Cuddle inside, add to 180.”

Play games. Use online interactive geometry exercises on parallel lines and transversals. Move the transversal. Watch angles change. Try gaming for logic at Lethal Weapon cast logic puzzles.

Or flashcards. One side: Diagram. Other: “Parallel? Yes/No. Why?”

More Practice Problems

Try these. Answers below, but think first.

1. Transversal crosses. Angle 1 (top-left top) 70°. Angle 5 (top-left bottom) 70°. Parallel?
2. Angle 4 (bottom-right top) 110°. Angle 6 (bottom-left bottom) 70°. Parallel?

Answers:

1. Yes, corresponding angles equal.
2. No. 110 + 70 = 180, but wrong pair. That is same-side if positions match, wait—check labels!

Build skills for how to determine if lines are parallel using corresponding angles. Practice more in Minecraft geometry hosting.

Slope and Parallel Lines (Quick Note)

In coordinate geometry, slope of parallel lines is the same. But for diagrams, stick to angles. No numbers needed here. Learn slopes in car tech guides.

Difference Between Angle Types

Clear up mix-ups:

• Corresponding angles: Same side of transversal, same position (both above or below).
• Alternate interior angles: Inside lines, opposite transversal sides.
• Alternate exterior angles: Outside, opposite.
• Interior and exterior angles: Inside between lines vs. outside.

See difference between alternate interior and corresponding angles. Corresponding can be anywhere. Alternate interior specific to inside. Compare in word roots.

Tips for Tests and Homework

• Read carefully: “Must be parallel” means proof needed³.
• Look at all given angles.
• One pair suffices.
• Draw lines if not clear.

This helps with geometry examples of lines cut by a transversal. Test tips in e-learning terms.

In Conclusion: Master the Diagram Hunt

You now know which diagram shows lines that must be parallel lines cut by a transversal. Use corresponding angles theorem, check alternate interior angles, and follow the steps. Practice with geometry diagrams and real examples. Soon, identifying parallel lines will be easy.

Remember the properties of parallel lines: equal or supplementary pairs from parallel lines cut by a transversal. This builds strong geometric reasoning.

What diagram stumps you most? Share in comments and practice more! For garden layouts using lines, see dream garden guide.

References

1. Gauthmath solution breakdown: https://www.gauthmath.com/solution/1765019652880390/Which-diagram-shows-lines-that-must-be-parallel-lines-cut-by-a-transversal-Lines – Step-by-step: Option with equal corresponding angles proves parallel; others do not. ↩︎
2. Brainly discussion on specific diagram choices: https://brainly.com/question/5372002 – Shows user questions with angle-labeled options; correct one has matching corresponding angles (both 115°). ↩︎
3. Quizlet flashcards on proving parallel: https://quizlet.com/ca/373393494/proving-lines-parallel-flash-cards/ – Reviews theorems with examples; emphasizes converse of corresponding angles. ↩︎